Detailed Scratchpad Prompting: LLMs As Interpreters

Method

I have often seen claims along the lines of "GPT-4 - despite being trained on trillions of tokens - is incapable of arithmetic, and is hence a lot dumber at this task than a calculator." This is a very weak critique.

After seeing this tweet, I wondered how hard it would be to make GPT-4 (or any LLM) do arithmetic on large numbers. Turns out it's not that hard at all! You just have to teach them how to do it like they're first graders and keep in mind that they're autoregressive models that benefit [1] from more information or space in the context. Here's a prompt I came up with and the interaction where GPT-4 does addition on large numbers (purple text = GPT-4 responses) very accurately:

example 1

3 7 8 + 6 4

index the digits

3 7 8

1: 3
2: 7
3: 8

6 4

1: 6
2: 4

number of digits in first operand = 3

number of digits in second operand = 2

3 > 2 => pad operand w/ fewer digits with abs(3 - 2) = 1 zero(s)

operand w/ fewer zeros: 6 4

padding step by step:

1 zero - 0 6 4

index the digits again

0 6 4

1: 0
2: 6
3: 4

3 7 8

1: 3
2: 7
3: 8

let | = concatenate, c = carry bit = 0, x = _, f = false, t = true

from last to first digit pair:

3: 8 + 4 + c = 12 + 0 = 12 -> c = 1 , d = 2 -> x = d | x = 2 | = 2 -> end? f
2: 7 + 6 + c = 14 + 1 = 15 -> c = 1 , d = 5 -> x = d | x = 5 | 2 = 5 2 -> end? f
1: 3 + 0 + c = 3 + 1 = 4 -> c = 0 , d = 4 -> x = d | x = 4 | 5 2 = 4 5 2 -> end? t

x = c | x = 0 | 4 5 2 = 0 4 5 2

0 4 5 2 is the answer

–––

example 2

2 2 2 + 7 7 7

index the digits

2 2 2

1: 2
2: 2
3: 2

7 7 7

1: 7
2: 7
3: 7

number of digits in first operand = 3

number of digits in second operand = 3

3 = 3 => no need to pad w/ zeros

let | = concatenate, c = carry bit = 0, x = _, f = false, t = true

from last to first digit pair:

3: 2 + 7 + c = 9 + 0 = 9 -> c = 0 , d = 9 -> x = d | x = 9 | = 9 -> end? f
2: 2 + 7 + c = 9 + 0 = 9 -> c = 0 , d = 9 -> x = d | x = 9 | 9 = 9 9 -> end? f
1: 2 + 7 + c = 9 + 0 = 9 -> c = 0 , d = 9 -> x = d | x = 9 | 9 9 = 9 9 9 -> end? t

x = c | x = 0 | 9 9 9 = 0 9 9 9

0 9 9 9 is the answer

index the digits

3 4 7 5 6 9 1 8 2 4 7 6 3 2

1: 3
2: 4
3: 7
4: 5
5: 6
6: 9
7: 1
8: 8
9: 2
10: 4
11: 7
12: 6
13: 3
14: 2

7 9 3 4 6 1 9 8 6 7 4 5 3 2 1 0 0 8 2

1: 7
2: 9
3: 3
4: 4
5: 6
6: 1
7: 9
8: 8
9: 6
10: 7
11: 4
12: 5
13: 3
14: 2
15: 1
16: 0
17: 0
18: 8
19: 2

number of digits in first operand = 14

number of digits in second operand = 19

14 < 19 => pad operand w/ fewer digits with abs(14 - 19) = 5 zero(s)

operand w/ fewer zeros: 3 4 7 5 6 9 1 8 2 4 7 6 3 2

padding step by step:

1 zero - 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2
2 zeros - 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2
3 zeros - 0 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2
4 zeros - 0 0 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2
5 zeros - 0 0 0 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2

index the digits again

0 0 0 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2

1: 0
2: 0
3: 0
4: 0
5: 0
6: 3
7: 4
8: 7
9: 5
10: 6
11: 9
12: 1
13: 8
14: 2
15: 4
16: 7
17: 6
18: 3
19: 2

7 9 3 4 6 1 9 8 6 7 4 5 3 2 1 0 0 8 2

1: 7
2: 9
3: 3
4: 4
5: 6
6: 1
7: 9
8: 8
9: 6
10: 7
11: 4
12: 5
13: 3
14: 2
15: 1
16: 0
17: 0
18: 8
19: 2

let | = concatenate, c = carry bit = 0, x = _, f = false, t = true

from last to first digit pair:

19: 2 + 2 + c = 4 + 0 = 4 -> c = 0 , d = 4 -> x = d | x = 4 | = 4 -> end? f
18: 3 + 8 + c = 11 + 0 = 11 -> c = 1 , d = 1 -> x = d | x = 1 | 4 = 1 4 -> end? f
17: 6 + 0 + c = 6 + 1 = 7 -> c = 0 , d = 7 -> x = d | x = 7 | 1 4 = 7 1 4 -> end? f
16: 7 + 0 + c = 7 + 0 = 7 -> c = 0 , d = 7 -> x = d | x = 7 | 7 1 4 = 7 7 1 4 -> end? f
15: 4 + 1 + c = 5 + 0 = 5 -> c = 0 , d = 5 -> x = d | x = 5 | 7 7 1 4 = 5 7 7 1 4 -> end? f
14: 2 + 2 + c = 4 + 0 = 4 -> c = 0 , d = 4 -> x = d | x = 4 | 5 7 7 1 4 = 4 5 7 7 1 4 -> end? f
13: 8 + 3 + c = 11 + 0 = 11 -> c = 1 , d = 1 -> x = d | x = 1 | 4 5 7 7 1 4 = 1 4 5 7 7 1 4 -> end? f
12: 1 + 5 + c = 6 + 1 = 7 -> c = 0 , d = 7 -> x = d | x = 7 | 1 4 5 7 7 1 4 = 7 1 4 5 7 7 1 4 -> end? f
11: 9 + 4 + c = 13 + 0 = 13 -> c = 1 , d = 3 -> x = d | x = 3 | 7 1 4 5 7 7 1 4 = 3 7 1 4 5 7 7 1 4 -> end? f
10: 6 + 7 + c = 13 + 1 = 14 -> c = 1 , d = 4 -> x = d | x = 4 | 3 7 1 4 5 7 7 1 4 = 4 3 7 1 4 5 7 7 1 4 -> end? f
9: 5 + 6 + c = 11 + 1 = 12 -> c = 1 , d = 2 -> x = d | x = 2 | 4 3 7 1 4 5 7 7 1 4 = 2 4 3 7 1 4 5 7 7 1 4 -> end? f
8: 7 + 8 + c = 15 + 1 = 16 -> c = 1 , d = 6 -> x = d | x = 6 | 2 4 3 7 1 4 5 7 7 1 4 = 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
7: 4 + 9 + c = 13 + 1 = 14 -> c = 1 , d = 4 -> x = d | x = 4 | 6 2 4 3 7 1 4 5 7 7 1 4 = 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
6: 3 + 1 + c = 4 + 1 = 5 -> c = 0 , d = 5 -> x = d | x = 5 | 4 6 2 4 3 7 1 4 5 7 7 1 4 = 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
5: 0 + 6 + c = 6 + 0 = 6 -> c = 0 , d = 6 -> x = d | x = 6 | 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
4: 0 + 4 + c = 4 + 0 = 4 -> c = 0 , d = 4 -> x = d | x = 4 | 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
3: 0 + 3 + c = 3 + 0 = 3 -> c = 0 , d = 3 -> x = d | x = 3 | 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
2: 0 + 9 + c = 9 + 0 = 9 -> c = 0 , d = 9 -> x = d | x = 9 | 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
1: 0 + 7 + c = 7 + 0 = 7 -> c = 0 , d = 7 -> x = d | x = 7 | 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 7 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? t

x = c | x = 0 | 7 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 0 7 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4

0 7 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 is the answer

The prompt contains one example of addition of a three digit and two digit number with instructions to pad the operand with fewer digits with zeros. The other example contained two three digit numbers, so no padding was required. But I then asked GPT-4 to add a 14 digit number with a 19 digit number and it did it correctly by following the template, padding the 14 digit number with 5 zeros. GPT-4 is clearly capable of addition. I'm surprised @pmddomingos didn't try to get GPT-4 to do some addition first. What's so wrong about expecting it do addition zero-shot without any chonky prompting like we see above?

Tokenization

We first look at the main reason why GPT-4 fails at zero-shot addition: the text input is tokenized using byte-pair encoding (BPE) [2], a compression algorithm introduced by Philip Gage in 1994. The text is split into subwords and there's a finite set - the vocabulary - of subwords that it is split into. Each subword - or token - has an id, and the text which is converted to a list of ids becomes the input to the GPT model. The way BPE works is by first doing a whitespace split on the BPE train corpus (some corpus with which you train the tokenizer). Then you set the vocab size you want and the tokenizer will then greedily merge the most frequent byte pairs until the vocab size is reached. This is now the vocabulary of the model.

The problem with this of course is that different numbers and digits appear with different frequencies in the BPE train corpus. So some number like '380' is a single token in the eye of GPT, whereas something like '381' gets split into two tokens '38' and '1' because '381' didn't occur that frequently. Since the BPE tokenizer first does a whitespace split, if you don't put a whitespace between each number in the prompt, GPT will not be able gauge what the digits of a number even are! So if you prompt GPT-4 '34756918247632 + 7934619867453210082', this is what it sees

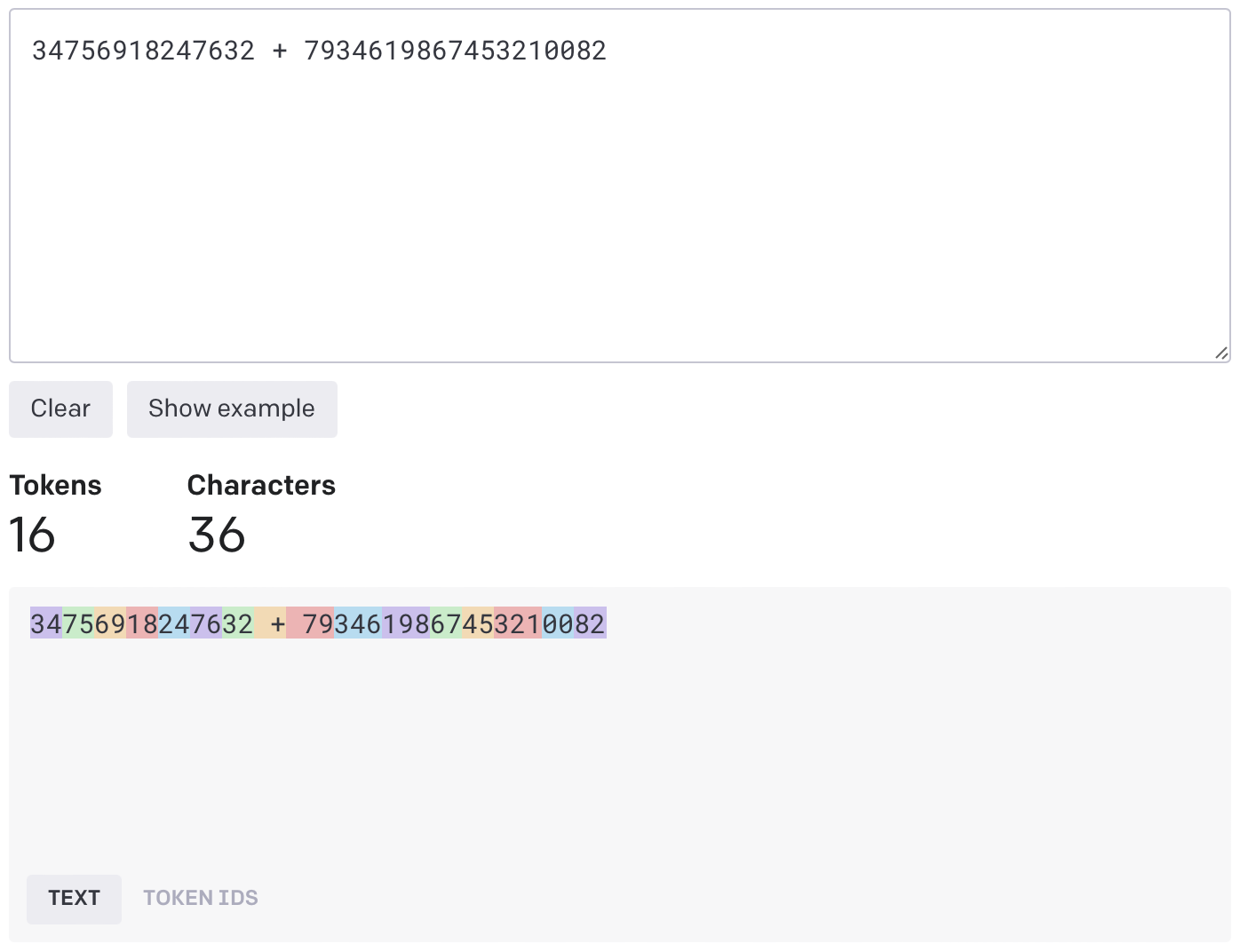
The different highlights are tokens from the vocabulary (around 100k tokens) and you can see how it is completely messed up. It's like if somebody told you that you can only add two numbers by zero-shot adding random chunks in each. If you split the digits by spaces however

Much better. Each digit is now a seperate token. And we ensure that we use whitespaces liberally in the addition template prompt, not just for the operands. I highly recommend nostalgebraist's post on BPE anomalies and Hugging Face's tutorial on BPE. If you're a Rust fanboi, you might also like this post about making BPE a lot more efficient (OpenAI's tiktoken uses Rust for example).

In-context learning

The second reason why GPT-4 fails at zero-shot addition is that you give it no room to do computation. GPT-4 is an autoregressive language model, which means that the output at a timestep is conditioned on all previous outputs. A language model is simply a probability distribution $p_{\theta}$ over a finite set of symbols $V$ (the vocabulary) where a symbol $s_t$ at timestep $t$ is sampled from the distribution $p_{\theta}(\cdot\,|\,s_1,\ldots, s_{t - 1}).$ This leads to the most important (IMO) emergent phenomena in large language models - in-context learning. It is the ability to utilise information in the previous context in non-trivial ways to predict the next token better. How does it happen here?

Well, how do first graders do addition? They go from right to left one digit at a time. Ask for the $n$th digit and they'll be able to count one by one and tell what it is. We need a way for our language model to retrieve a digit in any position like the first grader. So we first tell it to index all the digits. This lets it 1) get any digit given position and operand and 2) see how many digits are in each operand. Based on this, it can then figure out how many 0s it needs to pad the smaller number with

3 > 2 => pad operand w/ fewer digits with abs(3 - 2) = 1 zero(s)

We make it explicitly calculate the number of 0s to pad with. Then we do the padding step by step (or signal it to do it) like this

operand w/ fewer zeros: 6 4

padding step by step:

1 zero - 0 6 4

This is one step in the prompt. And look at how GPT-4 groks it

14 < 19 => pad operand w/ fewer digits with abs(14 - 19) = 5 zero(s)

operand w/ fewer zeros: 3 4 7 5 6 9 1 8 2 4 7 6 3 2

padding step by step:

1 zero - 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2
2 zeros - 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2
3 zeros - 0 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2
4 zeros - 0 0 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2
5 zeros - 0 0 0 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2

By first making it compute how many 0s it needs to pad with and then making it do the padding step by step with whitespaces, GPT-4 will know when to stop padding and move on to the next procedure. We make it re-index the digits like so

index the digits again

0 0 0 0 0 3 4 7 5 6 9 1 8 2 4 7 6 3 2

1: 0
2: 0
3: 0
4: 0
5: 0
6: 3
7: 4
8: 7
9: 5
10: 6
11: 9
12: 1
13: 8
14: 2
15: 4
16: 7
17: 6
18: 3
19: 2

7 9 3 4 6 1 9 8 6 7 4 5 3 2 1 0 0 8 2

1: 7
2: 9
3: 3
4: 4
5: 6
6: 1
7: 9
8: 8
9: 6
10: 7
11: 4
12: 5
13: 3
14: 2
15: 1
16: 0
17: 0
18: 8
19: 2

We then "define" some variables, let it know what they are, and set their initial values

let | = concatenate, c = carry bit = 0, x = _, f = false, t = true

and then we let it do the addition step by step, starting from the last digit pair going all the way to the first. We'll just look at the last few operations

4: 0 + 4 + c = 4 + 0 = 4 -> c = 0 , d = 4 -> x = d | x = 4 | 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
3: 0 + 3 + c = 3 + 0 = 3 -> c = 0 , d = 3 -> x = d | x = 3 | 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
2: 0 + 9 + c = 9 + 0 = 9 -> c = 0 , d = 9 -> x = d | x = 9 | 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? f
1: 0 + 7 + c = 7 + 0 = 7 -> c = 0 , d = 7 -> x = d | x = 7 | 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 7 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 -> end? t

x = c | x = 0 | 7 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 = 0 7 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4

0 7 9 3 4 6 5 4 6 2 4 3 7 1 4 5 7 7 1 4 is the answer

Putting the index at the front like 4:, 3:, etc., helps it retrieve the correct digit pair. Based on the sum of the pair, it "sets" the carry bit c and result digit d, like it's Python. The result digit d is then concatenated with the answer so far computed and we make the concat operation explicit as well. At the end of each line we have end? f/t to signify whether the procedure has ended and it needs to compute the final carry bit. It computes the final carry bit and concats it to the answer and we have our sum. Given two strings like '420' and '69', the Python implementation of the procedure we make GPT-4 use is as follows

def llm_add(a, b):
  if len(a) < len(b):
    a = '0' * abs(len(a) - len(b)) + a
  else:
    b = '0' * abs(len(a) - len(b)) + b
  x, result = '', ''
  template = '{}: {} + {} + c = {} + {} = {} -> c = {} , d = {} -> x = d | x = {} | {} = {} -> end?'
  c = 0
  for i in range(len(a) - 1, -1, -1):
    s = int(a[i]) + int(b[i]) + c
    d, c_, s_ = s % 10, s // 10, s + c
    x_ = f'{d}' if x == '' else f'{d} ' + x
    fin = (' t' if i == 0 else ' f') + '\n' 
    result += template.format(i + 1, a[i], b[i], s, c, s_, c_, d, d, x, x_) + fin
    x, c = x_, c_
  result += f"\nx = c | x = {c} | {x} = {str(c) + ' ' + x}"
  return result


print(llm_add('420', '69'))

and we can verify if GPT-4 used the correct procedure with a string match. One can view this through the lens of probabilistic programming [4]. Different sections of the context are traces of different subroutines, each spawned by the stochastic generation of specific tokens. The idea seems especially enticing considering ChatGPT Plugins and Code Interpreter, where the model literally calls APIs and uses an interpreter.

I think it's pretty clear that language models are unlike any kind of software we've previously built. GPT-4 does some weird combination of natural language processing and Python-like step by step interpretation here. It's a bit like we're emulating a virtual machine inside ChatGPT (the post now seems rather quiant in retrospect). There's a lot of debate on how best to view them - while some AI researchers claim language models are bogus, others turn them into Turing machines [3]. While some people decry that language models will be so capable so as to be existentially dangerous, it's pretty easy to show how weakly self-aware and incoherent their goals are.

The most useful analogy I've seen so far is Janus's simulators [5]: large language models are world simulators in text space. They are not calculators, they are not humans, but they can simulate both (to some extent). A clearer and more formal treatment of this viewpoint can be found in "Language Models as Agent Models" [6], and it's my preferred way of thinking about language models (especially RLHF-ed ones). You are behavior-cloning human activity on the internet; offline RL where the action space is the finite vocabulary of tokens.

The perspective comes with a host of positive and negative implications for language models which I'll go over in another post. For now, you'll know what to do if your calculator fails (you use a 1.76 trillion parameter mixture of experts model).

References

1. In-context Learning and Induction Heads ↩
2. A New Algorithm for Data Compression ↩
3. Memory Augmented Large Language Models are Computationally Universal ↩
4. Language Model Cascades ↩
5. Simulators ↩
6. Language Models as Agent Models ↩